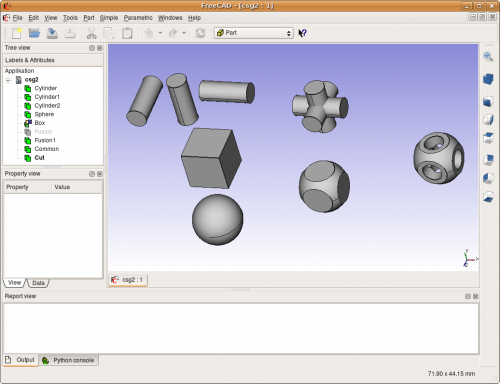
FreeCAD 中的 CAD 功能以 OpenCasCade 为核心。零件模块允许 FreeCAD 使用 OpenCasCade 的对象和函数。OpenCasCade 是一个专业级的 CAD 核心，它具有先进的三维几何操作和对象。零件对象不同于 Mesh Module 对象，它比网格对象复杂的多，因此允许更加先进的操作，如相干布尔运算操作、修改历史和有关参数的操作。
FreeCAD中零件形状的例子
工具
当你加载零件模块之后，将会出现“零件”菜单，零件模块工具就被放置在这个菜单中。
基本对象
下面是用于创建基本对象的工具。
修改对象
下面是一些可修改既有对象的工具。它们需要你选中欲处理的对象。
-
布尔运算：对选中的对象进行布尔运算（并、交、差） -
融合：对两个对象求并运算，合二为一 -
求交：提取两个对象的相交区域 -
剪切：从一个对象中去除另外一个对象与之相交的区域 -
拉伸：将一个对象的平面区域拉伸为实体 -
倒圆角：在对象的边界倒圆角 -
旋转体：将一个对象围绕一个轴向旋转成一个新的对象 -
截面：用一个截平面与一个对象求交，生成截面 -
倒斜角：在对象的边界倒斜角 -
镜像：对被选中的对象沿给定的轴向进行镜像复制
布尔运算
联合（融合）、求交（公共）和拆分（剪切）的例子
概念解释
在 OpenCasCade 术语中，我们将几何基元与（拓扑）形状区分开来。一个几何基元可以是一个点、一条直线、一个圆、一个平面等，或者像B样条曲线或曲面等一些更复杂的类型。一个形状可以是一个顶点、一条边、一条线、一个平面、一个实体或一个由其他形状组成的几何体。几何基元不可以直接显示在三维场景中，而是要被用作建筑几何学的形状。比如，一条边可以由一条线和一个圆的一部分来构成。
我们可以认为，几何基元是“无形的”构造单元，而形状才是建立在几何基元之上的真正的空间几何。
想得到一个关于它们的完整列表，可以参见 OCC documentation 并查找 Geom_Geometry 和 TopoDS_Shape。你也可以阅读更多关于几何对象与形状之间差异的资料。注意，不幸的是 OCC 文档不可在线使用（你必须下载存档），而且大多都是针对程序员而不是终端用户。但是值得庆幸的是你可以在这里找到足够的信息来开始你的使用之旅。
实际上，几何类型主要分为两类：曲线和面。利用曲线（线、圆、……）你可以直接创建一条边，利用面（平面、圆柱面、……）你可以直接创建一个表面。例如，几何基元线是无限的，也就是说，当它的形状必须是由初始点和终点来限制的时候，它就被定义为一个基向量和一个方向向量。一个立方体——一个实体可以由六个有限的面来创建。
由一条边和一个面也可以追溯到它的几何基元副本。
因此，由形状可以构建非常复杂的零件，或者反过来从一个复杂的形状中抽象出所有的子形状。
脚本
零件模块使用的主要数据结构是 OpenCascade 中的 BRep 数据结构。
关于零件模块的所有内容和对象类型现在都可以使用 python 脚本。其中包括几何基元，如线和圆（或弧），以及所有的拓扑形状，像顶点、边、线、面、实体和复合体。对其中的每一个对象，存在一些通用的创建方法，另外对于其中某些特殊的对象，尤其是拓扑形状，还存在像布尔运算/联合/拆分/交叉等先进的操作。若想了解更多有关零件模块的内容，可以参见 FreeCAD Scripting Basics 页面。
例子
创建一个线元素，切换到 Python 控制台并键入：
import Part,PartGui
doc=App.newDocument()
l=Part.Line()
l.StartPoint=(0.0,0.0,0.0)
l.EndPoint=(1.0,1.0,1.0)
doc.addObject("Part::Feature","Line").Shape=l.toShape()
doc.recompute()
让我们一步步的来分析以上的 python 实例：
import Part,PartGui doc=App.newDocument()
加载零件模块并创建一个新的文档
l=Part.Line() l.StartPoint=(0.0,0.0,0.0) l.EndPoint=(1.0,1.0,1.0)
线实际上是一条线段，因此既有初始点又有终点。
doc.addObject("Part::Feature","Line").Shape=l.toShape()
这样向文档中添加了一个零件对象类型，并将线段的形状表征指定为被添加对象的‘形状’特征。我们是用一个几何基元（the Part.line）由它来创建一个拓扑形状（the toShape() method），理解这一点非常重要。只有形状能够被添加到文档当中。在 FreeCAD 中，几何基元被当作形状的“建筑结构”来使用。
doc.recompute()
更新文档。这也准备了新零件对象的可视化表征。
注意，可以通过在构建器中指定初始点和终止点来创建一条线，例如，Part.Line(point1,point2)或者我们可以先创建一条默认的线，之后再设置它的特性，正如我们这里所做的那样。
可以用类似的方法来创建一个圆：
import Part
doc = App.activeDocument()
c = Part.Circle()
c.Radius=10.0
f = doc.addObject("Part::Feature", "Circle")
f.Shape = c.toShape()
doc.recompute()
再次注意，我们由它用圆（几何基元）来构成一个形状。我们当然也可以之后再进入构建器，这样做：
s = f.Shape e = s.Edges[0] c = e.Curve
Here we take the shape of our object f, then we take its list of edges, in this case there will be only one because we made the whole shape out of a single circle, so we take only the first item of the Edges list, and we takes its curve. Every Edge has a Curve, which is the geometry primitive it is based on.
如果想了解更多，清前往 Topological data scripting 页面。